增益平坦滤波片 (GFF),也称为增益均衡滤波片,用于在指定波长范围内平坦或平滑不等的信号强度。这种不等信号强度通常发生在放大阶段之后(例如,EDFA 和/或拉曼)。通常,GFF 与增益放大器一起使用,以确保放大的通道都具有相同的增益。GFF 的质量最好用峰-峰误差函数 (PPEF) 来描述,因为它代表了传输信号的最大平整度。通过将制造的滤波片的光谱性能与目标曲线的规格进行比较,计算出了该 PPEF 函数 。一般来说,能够达到最小的 PPEF 的决定因素是目标曲线的最大斜率和平滑度。部分应用程序需要多个扁平化区域,或在扁平区域外增加通带;这些可能会增加滤波片的复杂性。 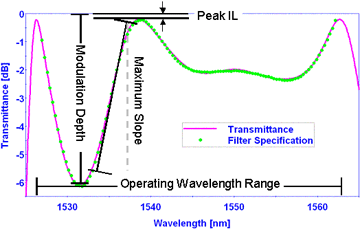
工作波长范围
增益均衡目标中指定的波长域通常定义其工作范围【开始, l结束】
插入损耗 (IL) 峰值【分贝】
插入损耗峰值是指在指定范围内的最大透射 (l最大值) 值。通常,指定范围为整个工作范围。IL 峰值 = T(l最大值)【分贝】例如:在工作范围内, IL 峰值< 0.1 分贝
调制深度 【分贝】
调制深度定义为在工作波长范围内的最大透射(T最大值)与最小透射值 (T最小值)【分贝】之间的差值 ,即: 调制深度 【分贝】 = T最大值 【分贝】 – T最小值【分贝】最大斜率【分贝/纳米】通过计算相邻目标点之间的斜率,得到斜率曲线。此计算在工作范围内的所有点上的最大值为最大斜率,即最大斜率 = Max{ ( T(li)【分贝】 – T(li-1)【分贝】)/ (li – li-1) }, i=1,2.3,…N
误差函数 【分贝】
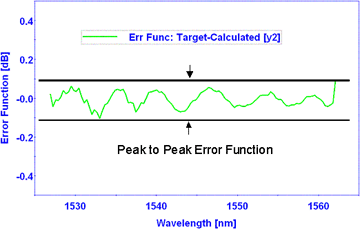
增益均衡曲线上的实测(T实测值) 【分贝】 与目标 (T目标值) 【分贝】 透射率点之间的差值定义了误差函数 (EF), 即, EF(li) 【分贝】 = T目标值(li) 【分贝】 – T实测值(li) 【分贝】
峰-峰误差函数 (PPEF) 【分贝】
峰-峰误差函数 (PPEF) 为一个单值规格,定义为最大误差函数(EF最大值)和最小误差函数 (EF最小值)之间的差值, 即, PPEF【分贝】= EF最大值 【分贝】 – EF最小值【分贝】 例如 PPEF < 0.4 分贝
偏振相关损耗 (PDL)【分贝】
对于给定波长的光,偏振相关损耗是指它在所有偏振状态下所观察到的透射率或反射率的最大变化。PDL 可根据光的偏振状态s和p的差值来计算。即:透射率 PDL (l) 【分贝】= Ts (l)【分贝】- Tp (l)【分贝】
GFF 形状系数
形状系数可以快速估计 GFF 曲线规格的复杂性。其定义为:形状因子=最大斜率/ PPEF。注:形状因子仅提供对 GFF 滤波片复杂性的相对度量。
基片标准具波纹效应【分贝】
对于相干光来说,任何种类的滤波片,当它两边的表面足够平行并且第二层表面未涂有增透 (AR) 膜时,都是一个法布里-珀罗标准具。在满足以上几个条件的情况下,就会有标准具波纹叠加在所需的滤波片形状上。对一个厚度为1毫米的基片来说,波纹在波长为 1550 纳米时的周期大约是 0.8 纳米。波纹大小取决于滤波片两边的反射情况和基片的平行度。减小标准具波纹的方法是引入足够大小的楔形角(> 0.4 度),还有一个方法就是在滤波片的第二层表面上镀一层非常好的增透膜。
